エントロピー（熱力学第二法則）【熱力学 2】

さて、熱力学第一法則により、密閉容器に閉じ込めた気体の内部エネルギー は、気体に加える熱 と、外力が気体にする仕事 の分だけ増加するということでした。式で書くと

でした。

しかし、熱とか仕事というのは全微分で表せない（＝始点から終点までの積分経路によって値が異なる＝始点の状態と終点の状態だけからは値が定まらない）ので ではなく で表記しました。

という話をしたのが前回↓
limnanthaceae.hatenablog.com

熱力学第一法則では、 であったので、残りの をどうにかする。

カルノーの定理

温度 の高温熱源から の熱を受け取り、温度 の低温熱源に の熱を流す熱機関を考えます。
不可逆機関の効率は可逆機関の効率より小さく、最大効率は作業物質によらず2つの温度のみで決定されます。
可逆機関の効率は

であり、不可逆機関の効率はこれより小さくなります。

エントロピー

カルノーの定理を変形すると

が成り立ちます。

Qの符号について、吸熱を正、放熱を負と再定義すると、

準静的＝可逆過程だと（不可逆とは？）多数のカルノーサイクルに分割できるので

つまり、極限的には周回積分

が成り立ちます。

ということは、

という積分は、どのような経路で積分しても成り立つということです。
例えば、状態A→状態B→状態C→状態D→状態Aという順番で一周する経路を考えます。

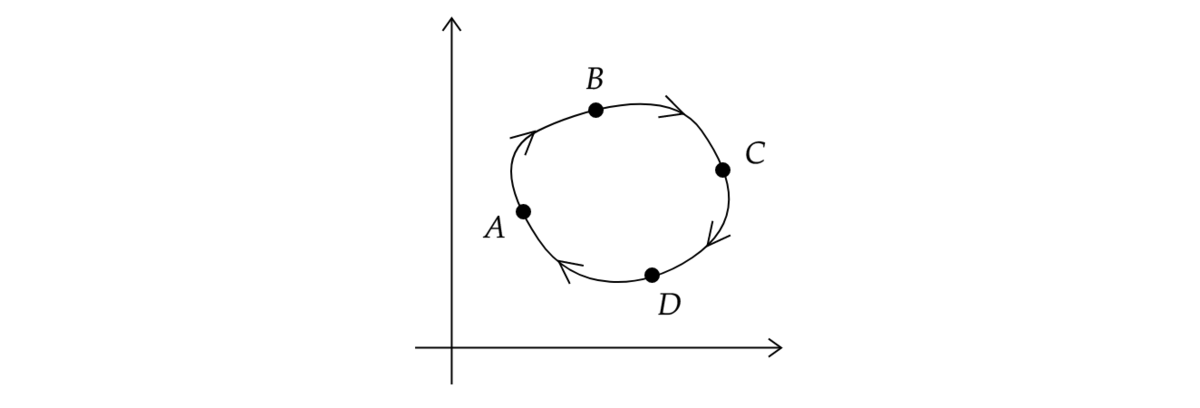
全体の周回積分が0なので、状態A→状態B→状態Cと状態C→状態D→状態Aの経路積分に分けて考えると

となり、

つまり、

なので、経路によらず状態A→状態Cの積分値は一致します。

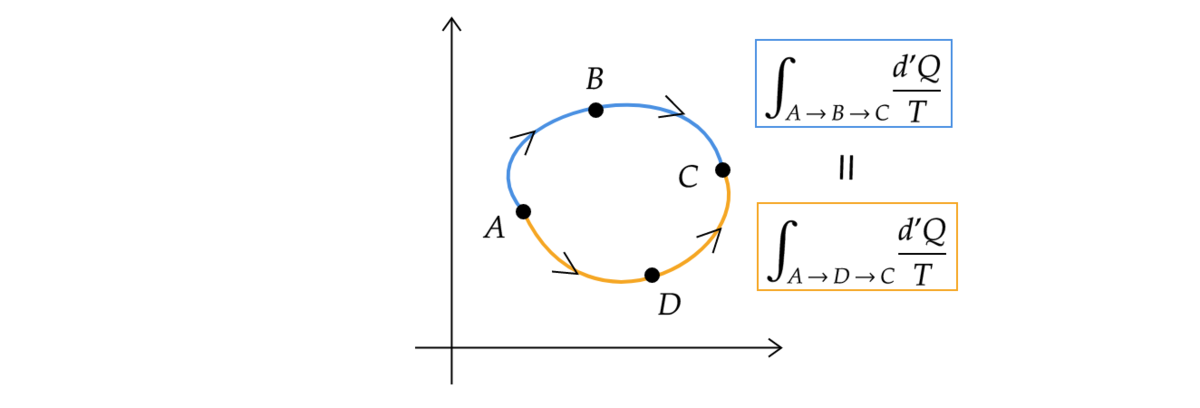
ので、エントロピー を

で定義すると、が状態量でないにもかかわらず、エントロピーは系の状態量になります。

ちなみに、エントロピーはこの微分形

で定義されることが多いです。

気体の内部エネルギーの微小変化

さて、エントロピーの微分値は

なので、 について整理すると

が得られます。

これと を に代入すると、気体の内部エネルギーの微小変化

が得られます。
これで全ての項が全微分で表すことができたので、この式を積分することで内部エネルギー を求めることができます（が、実際には は の関数であり、実測する必要がある）。