自由加群【環上の加群 5】 - リムナンテスは愉快な気分

環の時にもPIDだのUFDのEDだのクラスがたくさんありました。
加群にもその特性によって様々なクラスがあります。

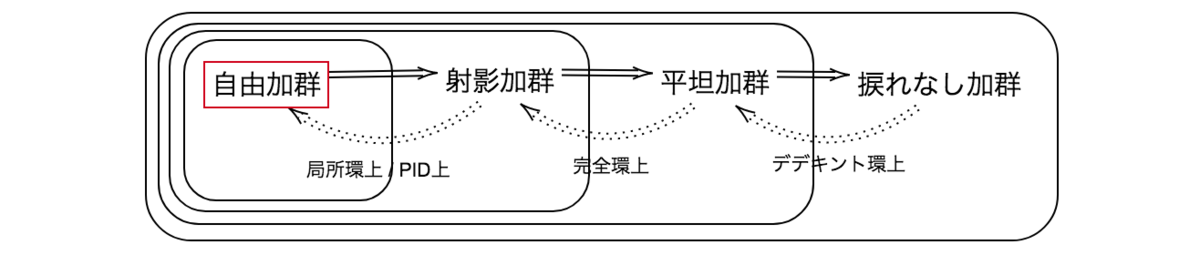
今回は最も基本的なクラスである自由加群について。
自由加群とは、基底を持つ加群のことである。

基底
自由加群
- 自由加群の例
- 自由加群でない例
階数
- 例

基底

ベクトル空間（線型空間）には必ず基底が存在しました（選択公理→Tukeyの補題から言える）。つまり、空間の全てのベクトルを表すことのできる一次独立（線型独立）なベクトルの集合があった。

しかし加群の場合、詳細は後述しますが必ずしも基底を持つとは限りません。基底を持たない加群と区別するために、基底を持つ加群＝ベクトル空間に限りなく近い加群は特別に自由加群と名付けられています。何がどう自由なのかよくわかりませんが、多分圏論をやればわかると思う。

基底を定義します。

def 5.1 $R$ -加群 $M$ の部分集合 $S=\{x_1,\cdots,x_n\}\subset M$ が $M$ の基底であるとは、
　(1) $S$ が $M$ を生成する
　(2) $S=\{x_1,\cdots,x_n\}$ が一次独立である
を満たすことである。

つまり、 $S$ が $M$ の一次独立な生成系なら、 $S$ は $M$ の基底。(1)は $S$ の元と $R$ の元を使って $M$ の全ての元を表すことができるということ、(2)は $M$ の元を $S$ の元と $R$ の元で一意に表せることを意味します。

もう少しちゃんと説明をすると、

(1) $M$ の任意の元 $x\in M$ が、 $S$ の元 $x_j$ に係数である $R$ の元 $a_j$ をかけたものの有限和（ $x=a_1x_1+a_2x_2+\cdots +a_jx_j$ ）で表すことができる
(2) $a_1x_1+\cdots +a_jx_j=0\in M$ であれば $a_1=\cdots=a_j=0\in R$

であるとき、 $S$ は $M$ の基底です。

自由加群

def 5.2 $R$ -加群 $M$ が基底を持つとき（つまり $M$ が一次独立な生成系 $S$ を持つとき）、 $M$ を自由 $R$ -加群という。

基底を持つ加群が自由加群。
つまるところ、 $R^I=\oplus_{i\in I}R$ と同型な加群が自由加群。
ベクトル空間は必ず基底を持ちましたが、加群は基底を持つとは限りません。なので、基底を持つか持たないかを区別します。

自由加群の例

$\mathbb{Z}[X]$ は自由 $\mathbb{Z}$ -加群

$\mathbb{Z}[X]$ は $X^n, n\in\mathbb{N}$ を不定元（変数）とした整数係数の多項式環のことです。
例えば $1, X, X^2, 2X+1\in\mathbb{Z}[X]$ 。

定義の $R=\mathbb{Z}$ 、 $M=\mathbb{Z}[X]$ とすると、
$\mathbb{Z}[X]$ の部分集合 $S=\{1,X,X^2,\cdots,X^n,\cdots\}$ は $\mathbb{Z}[X]$ を生成します。
また、 $S$ は $\mathbb{Z}$ 上一次独立です。
したがって、def 5.1 より $S$ は $M=\mathbb{Z}[X]$ の $\mathbb{Z}$ 基底なので def 5.2 より基底 $S$ を持つ $\mathbb{Z}[X]$ は自由 $\mathbb{Z}$ -加群となります。

ちなみに、 $R$ の元を各基底に掛けていると考えると、無限次元整数ベクトル空間と同一視できます。

なお便宜上、零加群 $\{0\}$ は空集合を基底とした自由加群と見なされます。

自由加群でない例

基底を持たない加群とはなんぞや、というお話。

$\mathbb{Q}$ は $\mathbb{Z}$ 上の加群だが、自由 $\mathbb{Z}$ -加群ではない

任意の2つの有理数 $a,b\in\mathbb{Q}$ を既約分数表示して

$a=\frac{p}{q}, b=\frac{r}{s}, (p,q,r,s\in\mathbb{Z})$
とすると、 $(qr)a-(sp)b=0$ であり $qr\neq 0, sp\neq 0$ なので一次従属。したがって基底があるとすれば1個しかないはずだが、全ての有理数を1つの有理数の整数倍で表すことはできない（＝ $\mathbb{Q}$ 全体を生成できる有理数は存在しない）ので $\mathbb{Q}$ は基底を持たない。

$\mathbb{Z}/n\mathbb{Z}$ は自由 $\mathbb{Z}$ -加群ではない

もう少し簡単な例。例えば $\mathbb{Z}/6\mathbb{Z}$ を考えます。
$6$ で割った余りが $n$ になる整数全体の集合を $\bar{n}$ とすると、集合として

$\mathbb{Z}/6\mathbb{Z}=\{\bar{0},\bar{1},\bar{2},\bar{3},\bar{4},\bar{5}\}$ と表記できます。ここで $\bar{1}$ に $0,1,2,3,4,5$ を掛けると $\mathbb{Z}/6\mathbb{Z}$ の元の全てを表すことができるので、 $\mathbb{Z}/6\mathbb{Z}$ は $\bar{1}$ で生成されると言えそうです。つまり、 $\langle\bar{1}\rangle=\mathbb{Z}/6\mathbb{Z}$ です。

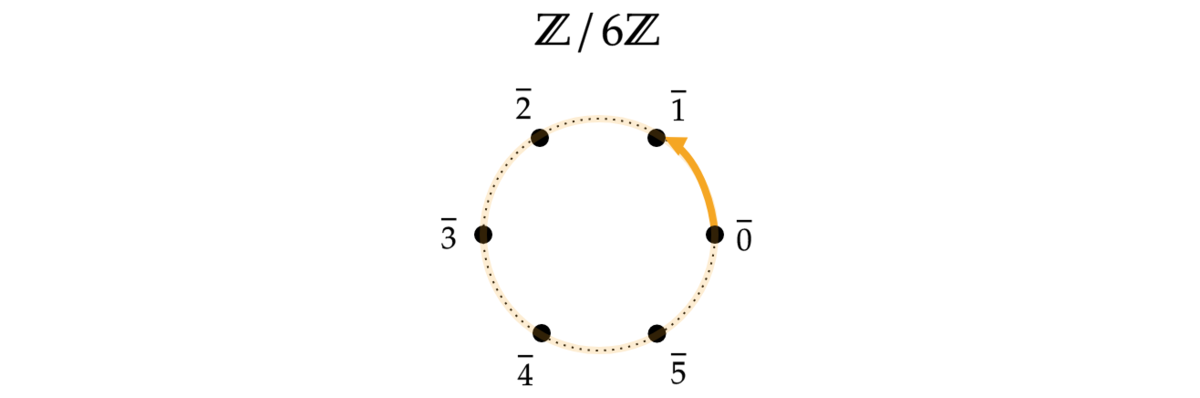
f:id:frecafloros:20210616232300p:plain

というわけで $\bar{1}$ は基底の候補です。しかし一方で、

$6\cdot\bar{1}=\overline{6\cdot 1}=\bar{6}=\bar{0}$ となるので、生成系 $\{\bar{1}\}$ は一次独立ではありません。

したがって生成系 $\{\bar{1}\}$ が基底ではないので、 $\mathbb{Z}/6\mathbb{Z}$ は自由 $\mathbb{Z}$ -加群ではありません。

階数

可換環で自由で基底があって基底として有限個で取れるとき、ベクトル空間の次元の概念が $R$ -加群で一般化される。
どういうことかというと、基底があるので自由加群の階数（rank）が定義できます。

def 5.3可換環 $R$ の有限生成自由 $R$ -加群 $M$ の基底の個数を $M$ の階数(rank)といい、 ${\rm rank}_R M$ と表す。

$R$ が「可換」であることがミソ。 $R$ が非可換環だとすると、 $R\simeq R^2$ がとれてしまったりするのでrankが定義できなくなる。

例

ガウス整数環 $\mathbb{Z}[i]$ について。
$\mathbb{Z}[i]$ は $\{1,i\}$ を基底に持つ自由 $\mathbb{Z}$ -加群であり、基底が2つなので $\mathrm{rank}_\mathbb{Z}\mathbb{Z}[i]=2$ といえます。

また、 $\{1,\sqrt{2},i,i\sqrt{2}\}$ は $\mathbb{Q}$ 上一次独立なので、

$M=\mathbb{Z}\oplus\mathbb{Z}\sqrt{2}\oplus\mathbb{Z}i\oplus\mathbb{Z}i\sqrt{2}$
という直和を考えると、 $M$ は $\{1,\sqrt{2},i,i\sqrt{2}\}$ を基底に持つ自由 $\mathbb{Z}$ -加群と言えます。
したがって $\mathrm{rank}_\mathbb{Z}M=4$ 。

また一方で、 $\{1,\sqrt{2}\}$ を基底に持つ自由 $\mathbb{Z}[i]$ -加群ともみなせるので、 $\mathrm{rank}_\mathbb{Z}\mathbb{Z}[i]=2$ 。