直積と直和【環上の加群 4】 - リムナンテスは愉快な気分

イスクイル飽きたので数学。

一次独立やらなんやらの前提。
加群と加群を合成して大きい加群をつくったり、複雑な加群を小さい加群の直積や直和の形に分解する。

直積
外部直和
内部直和

直積

def 4.1 $R$ ：可換環。2つの $R$ -加群 $M_1,M_2$ に対して直積集合 $M_1\times M_2$ 上に和とスカラー倍を（ $a\in R$ として）それぞれ

$(x_1,x_2)+(y_1,y_2)=(x_1+y_1,x_2+y_2)$ $a(x_1,x_2)=(ax_1,ax_2)$
と定義すると $M_1\times M_2$ は $R$ -加群となる。これを $M_1$ と $M_2$ の直積という。

ベクトルの和とスカラー倍と同じ。

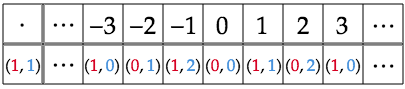
例えば加法剰余群 $\mathbb{Z}/2\mathbb{Z}, \mathbb{Z}/3\mathbb{Z}$ は $\mathbb{Z}$ -加群ですが、これらの直積 $\mathbb{Z}/2\mathbb{Z}\times\mathbb{Z}/3\mathbb{Z}$ を考えます。例えば $0,1\in\mathbb{Z}/2\mathbb{Z}, 1,2\in$ 和は

$(0,2)+(1,1)=(0+1,2+1)=(1,0)$
スカラー倍は
$4\cdot(1,2)=(4\cdot 1,4\cdot 2)=(0,2)$
となります。 $\mathbb{Z}/2\mathbb{Z}\times\mathbb{Z}/3\mathbb{Z}$ は $\mathbb{Z}$ -加群です。

和：

スカラー倍：

実は有限個の加群の直積と直和は一致するので $M_1\times M_2=M_1\oplus M_2$ *1。ですが、無限個の加群の場合、直積と直和は等しくない別概念になります*2。無限個の場合を考慮した一般の場合はdef 4.2のようになります。

def 4.2 $R$ ：可換環。 $R$ -加群の族 $\{M_\lambda\}_{\lambda\in\Lambda}$ に対して、直積集合 $\prod_{\lambda\in\Lambda}M_\lambda$ を考える。和とスカラー倍を（ $a\in R$ として）それぞれ

$(x_\lambda)+(y_\lambda)=(x_\lambda+y_\lambda)$ $a(x_\lambda)=(ax_\lambda)$
と定義すると $\prod_{\lambda\in\Lambda}M_\lambda$ は $R$ -加群となる。これを $\{M_\lambda\}_{\lambda\in\Lambda}$ の直積という。

「 $(x_\lambda)$ 」は「 $(x_1,x_2,\cdots)\in\prod_{\lambda\in\Lambda}M_\lambda, x_1\in M_1, x_2\in M_2,\cdots$ 」くらいの感覚。

外部直和

直和の定義。
直和には2種類あり、めんどくさいことに外部直和と内部直和がある。
「有限個の加群の直積と直和が一致する」というやつの直和は「外部直和」のこと。だと思う。というわけで外部直和の定義です。

def 4.3 $R$ -加群の族 $\{M_\lambda\}_{\lambda\in\Lambda}$ の直積 $\prod_{\lambda\in\Lambda}M_\lambda$ の部分加法群として、
$\begin{align}\bigoplus_{\lambda\in\Lambda}M_\lambda=\left\{(x_\lambda)\in\prod_{\lambda\in\Lambda}M_\lambda\middle| 有限個の\lambda を除いて x_\lambda=0\right\}\end{align}$ は $R$ -加群となる。これを $\{M_\lambda\}_{\lambda\in\Lambda}$ の（外部）直和という。

前述の通り $|\Lambda|<\infty$ のとき $\bigoplus_{\lambda\in\Lambda}M_\lambda=\prod_{\lambda\in\Lambda}M_\lambda$ 。「有限個の $\lambda$ を除いて」ということは選ぶ $\lambda$ は「0個」でもよいということで、有限個の加群の場合は直積と一致します。

なんでこんなめんどくさい定義の仕方をしているのかというと、普遍性がどうのこうのという話になってめんどくさいのでとりあえずスルーします。

また後述の内部直和と区別するために、こちらの外部直和を「 $\dot{\oplus}$ 」（上ドット付き）などで表記する場合があります。

内部直和

内部直和の定義。
初歩的な環上の加群論では直和といえば殆ど内部直和のことらしい。

さて、なんか適当な加群 $M$ の部分加群 $N_1,N_2\in M$ に対して、これらの和は

$N_1+N_2 = \{x_1+x_2\mid x_1\in N_1, x_2\in N_2\}$
でした。このとき $y\in N_1+N_2$ が $y=y_1+y_2$ の形に一意に表される時、 $N_1+N_2$ は直和である、つまり $N_1+N_2=N_1\oplus N_2$ と定義します。

def 4.4加群 $M$ に対して、部分加群 $N_1,N_2\subset M$ を考える。
$y\in N_1+N_2$ が $y_1\in N_1, y_2\in N_2$ に対して $y_1+y_2$ と一意に書けるとき、
$N_1+N_2 = N_1 \oplus N_2$

一般に、有限個の部分加群 $M_i\in M, (i=1,\cdots,n)$ の内部直和は次のように定義されます。

def 4.5 $M$ を $R$ -加群、 $\{M_i\}_{i=1,\cdots,n}$ を $M$ の部分加群の族とする。このとき、
$\begin{align}\sum_{i=1}^n M_i:=\{x_1+\cdots+x_n \mid x_1\in M_1\cdots,x_n\in M_n\}\end{align}$ は $M$ の部分加群となる。もし、 $\sum_{i=1}^n M_i$ の任意の元 $x$ が
$x=x_1+\cdots+x_n$ の形で表される時、 $\sum_{i=1}^n M_i$ は直和であるといい、
$\begin{align}\sum_{i=1}^n M_i=\bigoplus_{i=1}^n M_i\end{align}$ と表記する。

ある加群の部分加群で構成する（加群の「内部」で構成する）ので内部直和と呼ばれます。多分。
以降、外部直和を $\dot{\oplus}$ 、内部直和を $\oplus$ 、和を $+$ で表記します。

このとき次の定理が成り立ちます。

prop 4.6加群 $M$ の部分加群 $N_1,N_2\in M$ に対して、 $N_1+N_2=N_1\oplus N_2$ のとき、
$N_1\dot{\oplus} N_2\to N_1+N_2; (x_1,x_2)\mapsto x_1+x_2$ は全単射準同型。

prop 4.7加群 $M$ に対して、部分加群 $N_1,N_2\subset M$ を考える。このとき
$N_1\oplus N_2 \Leftrightarrow N_1\cap N_2 = \{0\}$

一般に、有限個の部分加群について次の4つは同値になります。

prop 4.8 $M$ を $R$ -加群、 $\{M_i\}_{i=1,\cdots,n}$ を $M$ の部分加群の族とする。

写像
$\begin{align}\dot{\bigoplus}_{i=1}^n M_i\to \sum_{i=1}^n M_i\end{align}$ $(x_1,\cdots x_n)\mapsto x_1+\cdots+x_n$ は全単射準同型。
$\sum_{i=1}^n M_i$ の任意の元 $x$ が $x_i\in M_i$ として $x=x_1+\cdots+x_n$ の形に一意に表せる。
$x_1+\cdots+x_n=0\Rightarrow x_1=\cdots=x_n=0$
$(M_1+\cdots+M_i)\cap M_{i+1} = \{0\}\,(i=1,\cdots,n-1)$