リムナンテスは愉快な気分

徒然なるままに、言語、数学、音楽、プログラミング、時々人生についての記事を書きます

トップ > ☆数学 > 加群の定義【環上の加群 1】

加群の定義【環上の加群 1】

☆数学

4ヶ月ぶりに加群やろうとしたらわからなくなりました。忘れました。
ノート見ても何もわかりません。というわけで、頭空っぽでもわかるような記事にしていきたい。
（群とか環とかくらいだとその辺にわかりやすい記事がたくさんあるのですが、流石に加群までくると解説してくれるサイトがあんまり無くて悲しいです。いやまあ真面目にやれという話ではあるんだけれども。）
ただあんまり誤魔化しすぎないようにはしたい。

加群論を始める前に

集合論→群論→環論・体論→加群論→ガロア理論→可換環論→古典的代数幾何→スキーム論→楕円曲線→数論幾何？

前提知識

群、環、体、あと線形代数とベクトル空間をちょっと知ってると面白いかもしれない。

で、結局「環上の加群」ってなんなん？

  • 「足し算」と「整数倍っぽいやつ」がなんかうまいことできるやつ
  • 線形代数、ベクトル空間の一般化
  • ホモロジー代数の前提
  • 可換環が作用している加法群（＝加群）の性質を調べる

動機付けはこんな感じで十分かな。
ベクトル空間は係数が体に対して定義されますが、加群は係数が環に対して定義されます。

記事一覧

  1. 加群の定義 (2020-12-27)
  2. 部分加群・有限生成 (2020-12-29)
  3. 準同型定理（第一同型定理） (2021-01-06)
  4. 直積と直和 (2021-03-08)
  5. 自由加群 (2021-06-19)
  6. ネーター加群・アルティン加群
  7. 表現行列
  8. PID上の加群
  9. 零化イデアル
  10. 単因子論
  11. アーベル群の基本定理
  12. ジョルダン標準形
  13. 射影加群
  14. テンソル積

参考資料

シリーズ全体で次の教科書・動画を参考にしています。

復習：ベクトル空間（線型空間）

ベクトル空間を一般化させたものが加群なのですが、ベクトル空間の定義は以下のようなものでした。


def 1.0V を空でない集合、\mathbb{K} を実数集合 \mathbb{R} または複素数集合 \mathbb{C} として、次の演算が定義されているとする：
(1) \mathbf{u},\mathbf{v}\in V に対して \mathbf{u}+\mathbf{v}\in V
(2) \mathbf{u}\in V, c\in \mathbb{K} に対して c\mathbf{u}\in V

また、\mathbf{u},\mathbf{v},\mathbf{w}\in V, a,b\in\mathbb{K} に対して以下の(1)〜(8)が成立しているとする：
(1) (\mathbf{u}+\mathbf{v})+\mathbf{w}=\mathbf{u}+(\mathbf{v}+\mathbf{w})
(2) \mathbf{u}+\mathbf{v}=\mathbf{v}+\mathbf{u}
(3) \exists\mathbf{0},\mathbf{v}+\mathbf{0}=\mathbf{v}
(4) \mathbf{v}\in V, \exists -\mathbf{v}, \mathbf{v}+(-\mathbf{v})=\mathbf{0}
(5) a(b\mathbf{u})=(ab)\mathbf{u}
(6) (a+b)\mathbf{u}=a\mathbf{u}+b\mathbf{u}
(7) a(\mathbf{u}+\mathbf{v})=a\mathbf{u}+a\mathbf{v}
(8) 1\mathbf{u}=\mathbf{u}

このとき、V は \mathbb{K}上のベクトル空間という。

ちなみに 0\mathbf{u}=\mathbf{0} を定義に入れる場合もありますが、(1),(2),(3),(4),(6)から導けますので基本はいらないです。

(6)に a=b=0 を代入して

(0+0)\mathbf{u}=0\mathbf{u}+0\mathbf{u}

つまり
0\mathbf{u}=0\mathbf{u}+0\mathbf{u}

ここで 0\mathbf{u} の逆元として (-0\mathbf{u}) というものを考え、両辺に足すと
0\mathbf{u}+(-0\mathbf{u})=(0\mathbf{u}+0\mathbf{u})+(-0\mathbf{u})

(1)より
0\mathbf{u}+(-0\mathbf{u})=0\mathbf{u}+(0\mathbf{u}+(-0\mathbf{u}))

(4)より 0\mathbf{u}+(-0\mathbf{u})=\mathbf{0} なので
\mathbf{0}=0\mathbf{u}+\mathbf{0}

(3)より 0\mathbf{u}+\mathbf{0}=0\mathbf{u}なので
\mathbf{0}=0\mathbf{u}

(2)より
0\mathbf{u}=\mathbf{0}


…こんなん覚えられるか！
って思わないんですかね数学強い人たちは（筆者は線形代数初習の時非常に苦しんだ記憶があります）。
まず前提条件がモリモリありますし、条件8個も覚えられなかったですね。


しかしすでに我々は群・環・体を習得しているわけで、群論・環論・体論の言葉で def 1.0 を解釈できるのです。
(1)〜(4)は V が結合律、可換律、加法単位元（零元）の存在、加法逆元の存在を満たす加法群であると言っているに過ぎないし、\mathbb{C} とか \mathbb{R} は結局のところ体ですので。つまりこうです。


def 1.0.1体 K、加法群 V とする。また、\mathbf{u},\mathbf{v}\in V, a,b\in K とする。
Kの作用 K\times V\to V; (a,{\bf v})\mapsto a{\bf v}が定義され、

(1) a(b\mathbf{u})=(ab)\mathbf{u}
(2) a(\mathbf{u}+\mathbf{v})=a\mathbf{u}+a\mathbf{v}、(a+b)\mathbf{u}=a\mathbf{u}+b\mathbf{u}
(3) 1\mathbf{u}=\mathbf{u}

を満たす時、V は K上のベクトル空間という。

まあこんだけですよ。ついでなので2つの分配法則も1つにまとめました。
この体 K を可換環 R\neq(0) に変えた（拡張した）のが加群です。

加群の定義

まずは加群の定義から。


def 1.1可換環 R\neq(0)、加法群 Mに対して Rの作用 R\times M\to M; (a,{\bf x})\mapsto a{\bf x}が定義され、
(1) (ab){\bf x}=a(b{\bf x})　（ a,b\in R, {\bf x}\in M）
(2) a({\bf x}+{\bf y})=a{\bf x}+a{\bf y}、 (a+b){\bf x}=a{\bf x}+b{\bf x}　（ a,b\in R, {\bf x},{\bf y}\in M）
(3) 1{\bf x}={\bf x}　（ 1=1_R\in R, {\bf x}\in M）
を満たす時、 Mを R-加群とする。

このとき、 Rの元をスカラーといい、写像 (a,{\bf x})\mapsto a{\bf x}をスカラー積といいます。
それから、スカラー積を導く写像のことをスカラー乗法といいます。多分。
わかりやすさのために加法群 Mの元は太字で表記したけど次回以降普通の書体にするかも。

嬉しい点は、線形空間（ベクトル空間）とは違って、体上だけでなく環上で定義できることだと思います。つまり、整数ベクトルみたいなものは（乗法逆元が閉じてないので）線形代数の範疇では扱えなかったけれども加群の範疇なら扱える。

加群の定義は、可換環Rと加法群Mに対して、(1) 環の乗法とスカラー乗法が両立し、(2) スカラー乗法の分配律が成り立ち、(3) スカラー乗法の単位元が存在すること。言い換えると、def 1.1 のようなスカラー乗法が定義できると環R上の加群Mが作れる。

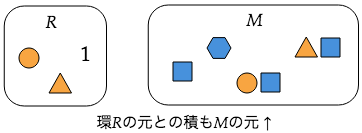
(1) 環の乗法とスカラー乗法が両立、つまり、「環 Rで乗算してからスカラー倍」と「スカラー倍のスカラー倍」が一致。

(2) スカラー乗法の分配律が成り立つ。

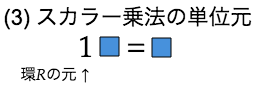
(3) スカラー乗法の単位元が存在。この単位元自体は環 Rの単位元。

加群の例

一般の加法群 Aを考えます。

可換環 R=\mathbb{Z}と見做して、自然な \mathbb{Z}倍（整数倍）をスカラー積とする。つまり、

m\in \mathbb{Z}, a\in Aに対し、

\begin{align}ma=\begin{cases}a+a+\cdots+a & (m>0, aがm個) \\ 0 & (m=0) \\ (-a)+(-a)+\cdots+(-a) & (m<0, (-a)が(-m)個)\end{cases}\end{align}

と定義すると Aは \mathbb{Z}-加群。

  • 整数ベクトル

まあ実際に加群を作って見ましょう。
意味がありそうな（ベクトル空間ではない）素朴な例は整数ベクトルとスカラー倍ではないでしょうか。
\mathbb{Z}が加法群なので、群の直積 \mathbb{Z}^2は演算を (a_1, a_2)+(b_1, b_2)=(a_1+b_1, a_2+b_2)と定義することで加法群。

次に、スカラー倍が\mathbb{Z}^2で閉じるような環を探します。
環として有理数 \mathbb{Q}や実数 \mathbb{R}を持ってくるとスカラー乗法が \mathbb{Z}^2で閉じないので、可換環には \mathbb{Z}を採用。

というわけで、R=\mathbb{Z}、M=\mathbb{Z}^2とします。
m\in\mathbb{Z}、(a,b)\in\mathbb{Z}^2に対してスカラー積をm(a,b)=(ma,mb)\in\mathbb{Z}^2（整数同士の積は整数）と定義でき、

(1) (mn)a=m(na)　（ m,n\in\mathbb{Z}, a\in\mathbb{Z}^2）
(2) m(a+b)=ma+mb、 (m+n)a=ma+na　（ m,n\in\mathbb{Z}, a,b\in\mathbb{Z}^2）
(3) 1a=a　（ 1\in\mathbb{Z}, a\in\mathbb{Z}^2）

が成り立つので、加群の定義を満たします。
なので、\mathbb{Z}^2は\mathbb{Z}-加群です。

可換環 R自身は R-加群。

  • 体 K

可換環R=K（体）、加法群Vとすると、 K-加群 Vはベクトル空間（ベクトル空間の定義から）*1。
ベクトル空間上のベクトルは伸び縮みできますが、加群（not ベクトル空間）の場合はベクトルを伸ばせるけど縮められない、あるいは縮める必要がないというイメージ（？）
可換環 Rが体でない場合は乗法逆元が存在しないので。

加群の性質

以下、 Rの零元は 0、 Mの零元は {\bf 0}と書きます。


prop 1.2 \forall a\in R, \forall {\bf x}\in Mに対して、
(1) a{\bf 0}={\bf 0}、 0{\bf x}={\bf 0}
(2) a(-{\bf x})=(-a){\bf x}=-(a{\bf x})

0\in R、 {\bf 0}\in M。

0に何を掛けても0だし、マイナスの掛け算は全体のマイナスであるという、それはそうなっててほしい性質ですが、加群の定義から証明できます。

(1)ですが、可換環 Rも加法群 Mも加法に関して群なので 0=0+0、 {\bf 0}={\bf 0}+{\bf 0}が使えます。
(2)は a{\bf x}+a(-{\bf x})={\bf 0}、 a{\bf x}+(-a){\bf x}={\bf 0}を導くことで a(-{\bf x})=-(a{\bf x})、 (-a){\bf x}=-(a{\bf x})を示します。
def 1.1の(2)より分配律が成り立つので a{\bf x}+a(-{\bf x})=a({\bf x}+(-{\bf x}))、 a{\bf x}+(-a){\bf x}=(a+(-a)){\bf x}が成り立ちます。


proof 1.2(1)
0=0+0より、
a{\bf 0}=a({\bf 0}+{\bf 0})-a{\bf 0}=a{\bf 0}+a{\bf 0}なので両辺からa{\bf 0}を引いて {\bf 0}=a{\bf 0}
同様に
0{\bf x}=(0+0){\bf x}=0{\bf x}+0{\bf x}なので両辺から 0{\bf x}を引いて {\bf 0}=0{\bf x}

(2)
a{\bf x}+a(-{\bf x})=a({\bf x}+(-{\bf x}))=a{\bf 0}={\bf 0}より a(-{\bf x})=-(a{\bf x})
a{\bf x}+(-a){\bf x}=(a+(-a)){\bf x}=0{\bf x}={\bf 0}より (-a){\bf x}=-(a{\bf x})

左加群・右加群

最後に、 Rが可換環でないとき、スカラー積が左側で乗算するのか、右側で乗算するのかが区別されます。


def 1.3Rが可換環でないとき、
・左側からのスカラー積R\times M\to M; (a,{\bf x})\mapsto a{\bf x}を満たすMを左R-加群、
・右側からのスカラー積M\times R\to M; ({\bf x},a)\mapsto {\bf x}aを満たすMを右R-加群
という。

例えば環R上のn\times n行列からなる正方行列環 M_n(R)は非可換なので、左から作用させれば左M_n(R)-加群、右から作用させれば右M_n(R)-加群。


→次：部分加群・有限生成【環上の加群 2】 - リムナンテスは愉快な気分

*1:左K-加群で十分？