リムナンテスは愉快な気分

徒然なるままに、言語、数学、音楽、プログラミング、時々人生についての記事を書きます

トップ > ☆数学 > 準同型定理（第一同型定理）【環上の加群 3】

準同型定理（第一同型定理）【環上の加群 3】

☆数学

加群にも群、環、体と同様に準同型、準同型定理があります。なので以降の議論は加群のみならず群や環と同等かと思われます。
群や環のときにも準同型については学んだと思いますが、改めて加群verの準同型定理（の復習）を見ていきましょう。

準同型

そもそもなんで準同型を考えるのかといえば、よくわからん加群の構造は直接調べなくとも、その加群と同型（全単射準同型）な加群を調べればわかるからなんですねぇ。


2つの加群を比較するとなったときどうするかというと、まあ写像で考えることになると思います。加群M_1から加群M_2への写像を\varphi :M_1\to M_2とすると、M_1は写像\varphiによる像{\rm Im}\varphi\subset M_2に写像されます。

f:id:frecafloros:20201231022051p:plain

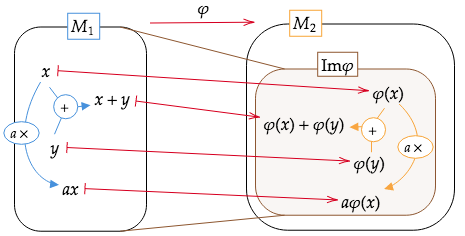
写像を噛ませたとしても加群としてだいたい「同じ」になってくれると嬉しいわけです。この、「ある程度の演算構造を保ってくれる写像」のことを準同型といいます。正確にはdef 3.1のように定義されます。


def 3.1R-加群M_1,M_2に対し、写像\varphi :M_1\to M_2が次の2つの条件
　(1)　\varphi(x+y)=\varphi(x)+\varphi(y)　(x,y\in M_1)
　(2)　\varphi(ax)=a\varphi(x)　　　　　(x\in M_1, a\in R)
を満たすとき、\varphiはR-準同型（写像）であるという。

(1)の左辺の+はM_1の、右辺のはM_2の加法です。
準同型で写した先もちゃんと加群になっていてほしいのですが、def 3.1のように定義すると\varphiで送った先の集合もうまいこと加群になってくれます。ただの群とは違い、スカラー乗法でも演算が閉じていないといけないので(2)の条件が必要です。

f:id:frecafloros:20201231022308p:plain

prop 2.2より、{\rm Im}\varphiがM_2の部分加群になる条件は、(1) {\rm Im}\varphiの元同士を足しても{\rm Im}\varphiの元、(2) {\rm Im}\varphiの元のスカラー倍も{\rm Im}\varphiの元です。
def 3.1のように準同型を定義すると、\varphi(x+y)も\varphi(ax)も{\rm Im}\varphiの元であることから、
　(1) \varphi(x),\varphi(y)\in{\rm Im}\varphiに対して\varphi(x)+\varphi(y)=\varphi(x+y)\in{\rm Im}\varphi
　(2) a\in Rに対してスカラー倍はa\varphi(x)=\varphi(ax)\in{\rm Im}\varphi
以上から{\rm Im}\varphiはM_2の部分加群です。つまり、準同型は和とスカラー倍を保つ写像になっているということです。


準同型が全単射のときはM_1の元とM_2の元が一対一対応するので{\rm Im}\varphi=M_2となります。このとき、\varphiは同型であり、M_1とM_2は同型であるといいます。


def 3.2M_1,M_2をR-加群とする。
\varphiが全単射準同型（\varphi ':M_2\to M_1も準同型）のとき、\varphiはR-同型といい、\varphi :M_1\xrightarrow{\cong}M_2のように書く。
また、R-同型\varphi :M_1\xrightarrow{\cong}M_2が存在するときM_1とM_2は同型であるといい、M_1\cong M_2と書く。


Rが体KのときK-加群は体K上のベクトル空間となりますが、同じようにK-準同型写像のはK-線形写像になります。


def 3.3Rが体Kのとき、K-準同型写像のことをK-線形写像ともいう。


準同型定理（第一同型定理）

準同型定理と第一同型定理は別物っぽいですが、第一同型定理のことを準同型定理と言っている参考書が結構多いです。
が、ここでは以降準同型定理改め第一同型定理で統一します。


同型であるような加群を作りたいわけですが、各元が一対一対応（全単射）かつ準同型なものを作りたい。\varphi :M_1\to M_2を準同型としたとき、\varphiが単射でない限り{\rm Im}\varphiはM_1より小さい（M_1より{\rm Im}\varphiの方が元の数が少ない）です。なので、{\rm Im}\varphiと同じ大きさになるようなM_1の部分加群を探す必要があります。

核・像・余核・余像

準備として、核（kernel）、像（image）、余核（cokernel）、余像（coimage）を改めて定義します（像は今まで平然と使っていましたが）。


def 3.4R-加群M_1,M_2に対してR-準同型が\varphi :M_1\to M_2のように定義されるとき、
　(1)　\varphiの核　{\rm Ker}\varphi=\{x\in M_1\mid\varphi(x)=0\}
　(2)　\varphiの像　{\rm Im}\varphi=\{\varphi(x)\mid x\in M_1\}
　(3)　\varphiの余核　{\rm Coker}\varphi=M_2/{\rm Im}\varphi
　(4)　\varphiの余像　{\rm Coim}\varphi=M_1/{\rm Ker}\varphi

f:id:frecafloros:20201231201634p:plain

ちなみに核{\rm Ker}\varphiはM_1のR-部分加群、像{\rm Im}\varphiはM_2のR-部分加群です。
スカラー倍に関して、x\in{\rm Ker}\varphiのときは\varphi(ax)=a\varphi(x)=a0=0よりax\in{\rm Ker}\varphiですし、\varphi(x)\in{\rm Im}\varphiのときa\varphi(x)=\varphi(ax)\in{\rm Im}\varphiなので、それぞれ{\rm Ker}\varphiと{\rm Im}\varphiが部分加群であることがわかります。

{\rm Coker}\varphiと{\rm Coim}\varphiはあまり使われず、大体の参考書などでそれぞれM_2/{\rm Im}\varphi, M_1/{\rm Ker}\varphiで表記されていると思います。第一同型定理では核{\rm Ker}\varphiが登場します。

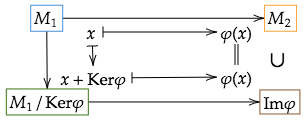
第一同型定理

第一同型定理、教科書やその他文書によっては準同型定理と書かれているかもしれないやつです（本来の準同型定理は第一同型定理よりも一般的な主張）。

加群M_1からM_2への準同型\varphiがあるとき、M_1を核{\rm Ker}\varphiで割った剰余加群M_1/{\rm Ker}\varphiは像{\rm Im}\varphi\subset M_2と同型となります。


prop 3.5 （第一同型定理）M_1,M_2をR-加群、\varphi :M_1\to M_2を準同型とする。
この時M_1の剰余加群M_1/{\rm Ker}\varphiから\varphiの像{\rm Im}\varphiへの全単射準同型が存在する。
つまり次のようなR-同型\overline{\varphi}が存在する：

\overline{\varphi}:M_1/{\rm Ker}\varphi\xrightarrow{\cong}{\rm Im}\varphi(\subset M_2); x+{\rm Ker}\varphi\mapsto\varphi(x)

\Leftrightarrow M_1/{\rm Ker}\varphiがM_1の部分加群、{\rm Im}\varphiがM_2の部分加群、M_1/{\rm Ker}\varphi\cong{\rm Im}\varphi。

prop 3.6は第一同型定理です。

f:id:frecafloros:20210102112816p:plain

第一同型定理、理解するまでは訳がわからないのですが、理解してしまえば自明としか思えなくなります（なりました）。


一般の準同型は（定義から）{\rm Im}\varphiに対して全射ですが単射とは限らないので、下図のように\varphi(x)に飛ぶM_1の元は複数あると考えられます。

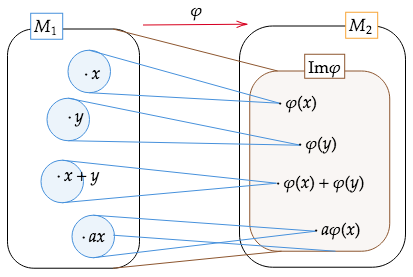
f:id:frecafloros:20210102213443p:plain

上の画像ではM_1の複数の元がM_2の元と対応しています。
さて、ここから頑張ってM_1を加工し同型（全単射準同型）を作ります。

とりあえず{\rm Im}\varphiへの全射ではあるので、単射にします。どうするかというと、「M_1の部分集合から{\rm Im}\varphiの元への写像」を作ります。こうすることで全単射が実現します。

で、\varphi(x)\in{\rm Im}\varphiへ飛ぶ元の集合を作りたいのですが、例えば

x+{\rm Ker}\varphi=\{x+k\mid k\in{\rm Ker}\varphi\}

がそれにあたります。つまり、準同型\varphiによって0\in M_2に飛ぶような元とxの和の集合を作ります。

f:id:frecafloros:20210102213528p:plain

{\rm Ker}\varphiがやっていることは、「同じ{\rm Im}\varphiの元に飛ぶM_1の元のグルーピング」。
そして、{\rm Ker}\varphiが部分加群なのでM_1/{\rm Ker}\varphiが剰余加群。x_i\in M_1とするとx_i+{\rm Ker}\varphiはM_1/{\rm Ker}\varphiの元です。剰余というものがうまいこと全単射準同型を導くような性質を持っています。あと\pi :M_1\to M_1/{\rm Ker}\varphiは全射。

kが{\rm Ker}\varphiの元とすれば\varphi(k)=0なので、\varphi(x+k)=\varphi(x)+\varphi(k)=\varphi(x)+0=\varphi(x)。
そして写像

\overline{\varphi}:M_1/{\rm Ker}\varphi\to{\rm Im}\varphi; x+{\rm Ker}\varphi\mapsto\varphi(x)

はR-同型（R-全単射準同型）。

f:id:frecafloros:20210102213621p:plain

一応\overline{\varphi}がR-同型であることを確認します。先の話から全単射ではあるので、和とスカラー倍に関してdef 3.1

\overline{\varphi}(\left(x+{\rm Ker}\varphi\right)+\left(y+{\rm Ker}\varphi\right))=\overline{\varphi}(x+{\rm Ker}\varphi)+\overline{\varphi}(y+{\rm Ker}\varphi)

\overline{\varphi}(a(x+{\rm Ker}\varphi))=a\overline{\varphi}(x+{\rm Ker}\varphi)

が成り立っていることを確認。


proof 3.5・和
\begin{align}\overline{\varphi}(\left(x+{\rm Ker}\varphi\right)+\left(y+{\rm Ker}\varphi\right))&=\overline{\varphi}(\left(x+y\right)+{\rm Ker}\varphi)\\&=\varphi(x+y)\\&=\varphi(x)+\varphi(y)\\&=\overline{\varphi}(x+{\rm Ker}\varphi)+\overline{\varphi}(y+{\rm Ker}\varphi)\end{align}



・スカラー倍
\begin{align}\overline{\varphi}(a(x+{\rm Ker}\varphi))&=\overline{\varphi}(ax+{\rm Ker}\varphi)\\&=\varphi(ax)\\&=a\varphi(x)\\&=a\overline{\varphi}(x+{\rm Ker}\varphi)\end{align}


というわけで次の定理もなりたちます。


prop 3.6{\rm Ker}\varphi=\{0\}\Leftrightarrow\varphiが単射。

準同型全体の集合


prop 3.7M_1,M_2をR-加群、{\rm Hom}_R(M_1,M_2)をM_1からM_2へのR-準同型の全体とする。
\varphi,\psi\in{\rm Hom}_R(M_1,M_2)とa\in Rに対して和とスカラー積を
\begin{align}(\varphi+\psi)(x)&=\varphi(x)+\psi(x) \\ (a\varphi)(x)&=a\varphi(x)\end{align}

と定義すると、{\rm Hom}_R(M_1,M_2)はR-加群。

いつか意味がわかるかもしれない。


proof 3.7(1) 環の乗法とスカラー乗法
\left(\left(ab\right)f\right)(x)=ab\left(f(x)\right)=a(bf)(x)=\left(a(bf)\right)(x)

(2) スカラー乗法の分配律
\left(a\left(f+g\right)\right)(x)=a\left(\left(f+g\right)(x)\right)=a\left(f(x)+g(x)\right)=af(x)+ag(x)=(af)(x)+(ag)(x)
\left((a+b)f\right)(x)=(a+b)f(x)=af(x)+bf(x)=(af)(x)+(bf)(x)

(3) スカラー乗法の単位元
(1f)(x)=1f(x)=f(x)


↑初：加群の定義【環上の加群 1】 - リムナンテスは愉快な気分
←前：部分加群・有限生成【環上の加群 2】 - リムナンテスは愉快な気分
→次：https://limnanthaceae.hatenablog.com/entry/2021/03/08/003000