トロピカル代数で機械学習〜トロピカル回帰直線を作る〜【理論編】

皆さんは「トロピカル幾何」とか「トロピカル演算」とか「トロピカル代数」というものをご存じでしょうか。

名前からして面白そうだなぁ～とは思いつつ、何に使うかさっぱり分かりませんでした。ですが、先日面白い記事を見つけました。トロピカル演算を使うとグラフの最短経路問題が解けるみたいで。
qiita.com

そんなわけで「最短経路問題のアルゴリズムが開発されてるなら機械学習も当然あるよね」と。

で、調べてみると、最近の研究*1によると、トロピカル演算を用いた

深層学習
確率グラフィカルモデル
線形回帰

というのが既に開発されているようです*2。

というわけで、我々はトロピカル線形回帰の奥地へと進むのであった…

この記事の方針

厳密な数学的議論というよりは、「数学的に理解する」ことを優先します。
途中、論証がガバい箇所があります。でも赦してください。

忙しい人向け

トロピカル連立方程式を解くのは難しい(逆行列を定義するためにテクニカルなことをする必要がある)
双対演算を導入すると双対なベクトル変換がガロア接続になる
ガロア接続の性質を使ってGLE(greatest lower estimate)→MMAE(minimum max absolute error)の順に回帰係数を推定する

普通の単回帰（最小二乗法）

復習ということで、通常の演算による通常の単回帰をおさらいします。

$N$ 個の入力データ $(x_i, y_i)$ があるとします。

このデータを直線 $y=ax+b$ に単回帰したいとします。ここで、実際にはデータがきれいに直線に乗ることはあり得ず幾らかノイズ（誤差）が入るはずなので、各データの回帰値と観測値の誤差を $\varepsilon_i$ とすると、
\begin{align}
y_i = (ax_i+b)+\varepsilon_i
\end{align}
という関係になっているはずです。最小二乗法では、データ全体で、この誤差の2乗の和が最小になってほしいので、
\begin{align}
\|\varepsilon\|_2=\|ax_i+b-y_i\|_2=\sum_i^N(ax_i+b-y_i)^2
\end{align}
を最小化すればよいということでした（別に二乗じゃなくても何でもいいのですが、微分しやすいので二乗です）。
最終的には $a,b$ でそれぞれ偏微分して $0$ になるところが $\|\varepsilon\|_2$ の最小値なので、頑張って解くと解けます*3。

単回帰の場合、行列で書くと
\begin{align}
\label{eq:vecdef}
\boldsymbol{X} =
\begin{bmatrix}
x_1 & 1 \\
\vdots & \vdots \\
x_N & 1
\end{bmatrix}
, \quad
\boldsymbol{w} =
\begin{bmatrix}
a \\
b
\end{bmatrix}
, \quad
\boldsymbol{y} =
\begin{bmatrix}
y_1 \\
\vdots \\
y_N
\end{bmatrix}
\end{align}
から、誤差
\begin{align}
\|\boldsymbol{X}\boldsymbol{w}-\boldsymbol{y}\|_2
\end{align}
を最小にする $\boldsymbol{w}$ を導出すればよく、 $\boldsymbol{w}$ で偏微分して0になることを考えると、推定値 $\hat{\boldsymbol{w}}$ は結局
\begin{align}
\hat{\boldsymbol{w}}=(\boldsymbol{X}^\top \boldsymbol{X})^{-1} \boldsymbol{X}^\top \boldsymbol{y}
\end{align}
を計算すればよいということになります。

トロピカルな単回帰

さて、トロピカル版の線形単回帰をやっていきます。その前に「トロピカル半環」を定義します。

トロピカル半環とは、実数に無限小を加えた集合 $\mathbb{R}\cup\{-\infty\}$ に対して、加法をmax関数、乗法を + （通常の加法）で定義した代数構造（Max-plus 代数）です*4。以降、トロピカル加法を $\oplus$ 、トロピカル乗法を $\otimes$ と表記すると、トロピカル半環における加法と乗法は $a,b\in \mathbb{R}\cup\{-\infty\}$ に対して
\begin{align}
a \oplus b & := \max(a,b) \\
a \otimes b & := a + b
\end{align}
と定義されます（半環とは環から加法逆元を除いた代数構造です）。
ちなみに実数に無限小 $-\infty$ を加えているのは、これが加法零元（「ゼロ」）だからです。つまり、どんな数 $a$ に対しても、トロピカル加法で $-\infty$ を足しても $a$ のままです（計算してみてください）。

というわけで、今回回帰したい（一変数）トロピカル直線は
\begin{align}
y=a \otimes x \oplus b = \max (a+x, b)
\end{align}
となります。

さて、 $N$ 個の入力データ $(x_i, y_i)$ が上記のトロピカル直線に乗っているとします。行列 $\boldsymbol{X}$ 、ベクトル $\boldsymbol{w}, \boldsymbol{y}$ を
\begin{align}
\boldsymbol{X} =
\begin{bmatrix}
x_1 & 0 \\
\vdots & \vdots \\
x_N & 0
\end{bmatrix}
, \quad
\boldsymbol{w} =
\begin{bmatrix}
a \\
b
\end{bmatrix}
, \quad
\boldsymbol{y} =
\begin{bmatrix}
y_1 \\
\vdots \\
y_N
\end{bmatrix}
\end{align}
とします。式\eqref{eq:vecdef}と違って $\boldsymbol{X}$ の2行目が $0$ なのは、トロピカル乗法の単位元が $0$ であることに依ります（任意の元 $a$ にトロピカル乗法で $0$ を掛けても $a$ 、つまり、 $a \otimes 0 = a + 0 = a$ だし $0 \otimes a = 0 + a = a$ が成り立つ）。したがって、連立方程式としては行列形式で
\begin{align}
\label{eq:tpprob}
\boldsymbol{X} \circledcirc \boldsymbol{w} = \boldsymbol{y}
\end{align}
と表すことができます。新たな記号 $\circledcirc$ が出現しましたが、これはトロピカル版の行列積で*5、例えば、行列 $A,B$ の積の $ij$ 要素は
\begin{align}
[\boldsymbol{A}\circledcirc\boldsymbol{B}]_{ij}=\oplus_{k=1}^N (a_{ik} \otimes b_{kj})=\max_k(a_{ik} + b_{kj})
\end{align}
と計算されます。これだけを見ると何だかよく分からない気もしますが、実は通常の行列積の計算方法の加法と乗法をトロピカル化しただけで、具体例で言えば、式\eqref{eq:tpprob}を計算すると、
\begin{align}
\boldsymbol{X} \circledcirc \boldsymbol{w} =
\begin{bmatrix}
x_1 & 0 \\
\vdots & \vdots \\
x_N & 0
\end{bmatrix}
\circledcirc
\begin{bmatrix}
a \\ b
\end{bmatrix}
=
\begin{bmatrix}
(x_1 \otimes a) \oplus b \\
\vdots \\
(x_N \otimes a) \oplus b
\end{bmatrix}
=
\begin{bmatrix}
y_1 \\
\vdots \\
y_N
\end{bmatrix}
= \boldsymbol{y}
\end{align}
のように式変形することができます。

本題に戻りまして、我々が何をしたかったかというと、トロピカル回帰係数 $\boldsymbol{w}$ の推定でした。というわけで何か適当な $\ell_p$ -ノルムで
\begin{align}
\|\boldsymbol{X} \circledcirc \boldsymbol{w} - \boldsymbol{y}\|_p
\end{align}
を最小化するような $\boldsymbol{w}$ を計算すればよいわけです。

…と言いたいところですが、残念なことに、通常の線形回帰のようには計算できません。何故かというと、トロピカル半環には逆元が存在しないからです。どういうことかというと、 $a$ に何か足したら $-\infty$ （＝トロピカル演算におけるゼロ）になるような都合のいい $”-a”$ みたいな元が存在しないということです。もしあるなら
\begin{align}
a \oplus (“-a”) = \max(a, “-a”) = -\infty
\end{align}
が成り立つはずですが、そんな $-a$ はどうやら無さそうです（maxをとるので、任意の $x$ に対して $a \oplus x\leq a>-\infty$ $）。従って逆元がないから微分したり逆行列を定義することができません。解けません。困りました。

拡張

今まで $\mathbb{R}\cup\{-\infty\}$ に対する加法（ $\oplus:=\max$ ）と乗法（ $\otimes:=+$ ）のMax-plus演算を考えてきたのですが、逆元がないなら逆元っぽいのを作ってしまえばよいのです。

Max-plus代数は、実数に無限小を加えた集合 $\mathbb{R}\cup\{-\infty\}$ に対して、加法をmax関数、乗法を + （通常の加法）で定義した代数構造でした。また、加法零元は $\epsilon=-\infty$ 、乗法単位元は $e=0$ でした。まとめると、
\begin{align}
\mathbb{R}\cup\{-\infty\},\quad a \oplus b := \max(a,b), \quad a \otimes b := a + b, \quad \epsilon:=-\infty, \quad e:=0
\end{align}

ところで、 $\max$ と似ている関数がありますよね。そうですね、 $\min$ ですね。
Max-plus代数の集合を $\mathbb{R}\cup\{\infty\}$ に、加法と加法零元を $\ominus := \min, \epsilon':=\infty$ に換え、乗法、乗法単位元はそのまま（ $\oslash := +, e':=0$ ）にすると、Max-plusと同様*6の体系、Min-plus代数を構成することができます。まとめると、
\begin{align}
\mathbb{R}\cup\{\infty\},\quad a \ominus b := \min(a,b), \quad a \oslash b := a + b, \quad \epsilon':=\infty, \quad e':=0
\end{align}
です。

Max-plus代数とMin-minus代数を合体させることで、あたかも加減乗除が揃ったような体系を構築することができるのですが、これらを一体の体系として扱うにはもう少し工夫が必要になります。特に、今回逆元が無くて困ってたので、これを解決したい。というわけで、例えば、 $\max_i(\cdot)$ を $\min_i(\cdot)$ を使って表すとどうなるでしょうか。 $a,b\in\mathbb{R}\cup\{-\infty\}$ とすると、
\begin{align}
\max(a,b)=-\min(-a,-b)
\end{align}
が成り立ちます。マイナスを取る操作を $a^*(=-a)$ のように表記して、これを共役元ということにすると、
\begin{align}
a \oplus b=(a^* \ominus b^*)^*
\end{align}
と書き直せます。また、通常の加法に対して
\begin{align}
a+b = -( (-a)+(-b) )
\end{align}
なので
\begin{align}
a \otimes b=(a^* \oslash b^*)^*
\end{align}
が成り立ちます。 $\infty^*=-\infty$ についても成り立ちます。

今回はMax-plus代数をベースに構築したので、Min-plus代数の方を「双対」なものとします。ここまでに出てきた要素を一覧にしたものが以下の表です。

項目	記号	意味
集合		$\mathbb{R}\cup\{\pm\infty\}$
加法	$\oplus$	$\max$
零元	$\epsilon$	$-\infty$
双対加法	$\ominus$	$\min$
双対零元	$\epsilon'$	$\infty$
乗法	$\otimes$	$+$
単位元	$e$	$0$
双対乗法	$\oslash$	$-$
双対単位元	$e'$	$0$
共役元	$a^*$	$-a$

最適解

ここまでくると、双対行列積（＝Min-plus側の行列積）も定義することができまして、
\begin{align}
[\boldsymbol{A}\circledast\boldsymbol{B}]_{ij}:=\ominus_{k=1}^N (a_{ik} \oslash b_{kj}) = \min_k(a_{ik}+b_{kj})
\end{align}
と定義することにします。で、
\begin{align}
\boldsymbol{X} \circledcirc \boldsymbol{w} = \boldsymbol{y}
\end{align}
が解をもつなら、最大元 $\hat{\boldsymbol{w}}$ は
\begin{align}
\hat{\boldsymbol{w}}=\boldsymbol{X}^* \circledast \boldsymbol{y} = \left[\ominus_{i=1}^N(x_{ij}^* \oslash y_i)\right] = \left[\min_{i}(y_i - x_{ij})\right]
\end{align}
で計算することができるらしいです。イメージとしては擬逆行列 $\boldsymbol{X}^*$ と思ってしまってもいいとは思いますが、厳密には、行列積 $\circledcirc, \circledast$ がガロア接続という関係にあることから導き出されます。

ガロア接続

2つの半順序集合 $(A,\leq), (B,\leq)$ があったとします。
また、写像 $F: A\to B, G:B\to A$ を単調増加写像 *7とします。
は
このとき、任意の $a\in A$ や $b\in B$ に対し、
\begin{align}
F(a) \leq b \Leftrightarrow a \leq G(b)
\end{align}
が成り立つとすれば、これをガロア接続と呼びます。

ガロア接続には激ヤバ性質がありまして、 $\forall b\in B, \{a \in A \mid F(a) \leq b\}$ の最大元は $G(b)$ です*8。

で、実は行列積 $\circledcirc, \circledast$ は互いにガロア接続の関係にあるため*9、この性質を使えます。ここで、それぞれの作用を
\begin{align}
\delta(\boldsymbol{w}) & :=\boldsymbol{X}\circledcirc\boldsymbol{w} \\
\varepsilon(\boldsymbol{y}) & :=\boldsymbol{X}^* \circledast\boldsymbol{y}
\end{align}
と定義します。そうすると、 $\delta(\boldsymbol{w}), \varepsilon(\boldsymbol{w})$ はガロア接続なので、
\begin{align}
\boldsymbol{X}\circledcirc\boldsymbol{w} = \delta(\boldsymbol{w}) \leq \boldsymbol{y} \Leftrightarrow \boldsymbol{w} \leq \varepsilon(\boldsymbol{y}) =\boldsymbol{X}^* \circledast\boldsymbol{y}
\end{align}
が成り立ちます。

GLE (greatest lower estimate)

$\|\boldsymbol{X}\circledcirc\boldsymbol{w} - \boldsymbol{y}\|_p$ を最小化しますが、 $\boldsymbol{X}\circledcirc\boldsymbol{w} \leq \boldsymbol{y}$ としても状況は変わらないので、この仮定を入れます。先ほどの $\delta, \varepsilon$ がガロア接続なので、
\begin{align}
\boldsymbol{w} \leq \boldsymbol{X}^* \circledast\boldsymbol{y}
\end{align}
ですが、 $\|\boldsymbol{X}\circledcirc\boldsymbol{w} - \boldsymbol{y}\|_p$ を小さくするには $\boldsymbol{X}\circledcirc\boldsymbol{w} \leq \boldsymbol{y}$ なので $\boldsymbol{X}\circledcirc\boldsymbol{w}$ をできるだけ大きめに取りたい。

というわけで、 $\boldsymbol{w}$ の最大元は $\boldsymbol{X}^* \circledast\boldsymbol{y}$ で計算できるので、最小 $\ell_p$ 誤差に関する最適値 $\hat{\boldsymbol{w}}$ は、
\begin{align}
\hat{\boldsymbol{w}} =
\begin{bmatrix}
\hat{a} \\ \hat{b}
\end{bmatrix}
&= \boldsymbol{X}^* \circledast \boldsymbol{y} \\
&=
\begin{bmatrix}
-x_1 & \cdots & -x_N \\
0 & \cdots & 0
\end{bmatrix}
\circledast
\begin{bmatrix}
y_1 \\
\vdots \\
y_N
\end{bmatrix} \\
& =
\begin{bmatrix}
\min_i (y_i-x_i) \\
\min_i (y_i)
\end{bmatrix}
\end{align}
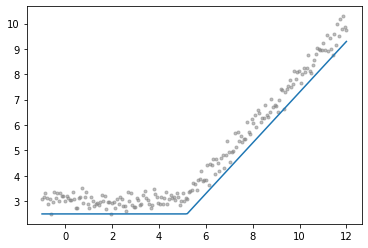
となります。幾何的には、データの下限にfitします。

MMAE (minimum max absolute error)

GLEによるトロピカル回帰ではデータの下限にfitしますが、もうちょいいい感じに回帰させたいわけですね。

じゃあどうするかということですが、最小 $\ell_\infty$ 誤差の下でより良い近似解を得ます。 $\boldsymbol{X} \circledcirc\boldsymbol{w}=\boldsymbol{y}$ の最大元 $\hat{\boldsymbol{w}}$ に対する $\ell_\infty$ 誤差を
\begin{align}
\|\boldsymbol{X} \circledcirc \hat{\boldsymbol{w}} - \boldsymbol{y}\|_\infty=\|\boldsymbol{X} \circledcirc (\boldsymbol{X}^* \circledast \boldsymbol{y}) - \boldsymbol{y}\|_\infty
\end{align}
で評価できます。これは、GLE回帰直線と観測された $\boldsymbol{y}_i$ との差の中で最大のものを計算していることになります*10。これを $2\mu$ と置くと、
\begin{align}
\mu = \frac{1}{2}\|\boldsymbol{X}\circledcirc\hat{\boldsymbol{w}}-\boldsymbol{y}\|
\end{align}
は、GLE回帰直線からデータの中心線あたりまでの距離に相当します。この考え方をMMAE (minimum max absolute error)と呼び、MMAEによる回帰係数の推定値 $\tilde{\boldsymbol{w}}$ は
\begin{align}
\tilde{\boldsymbol{w}} &= \hat{\boldsymbol{w}} + \mu \\
&= \boldsymbol{X}^* \circledast \boldsymbol{y} + \mu
\end{align}
で計算されます。結局、トロピカル直線 $y=(a \otimes x) \oplus b=\max(a+x, b)$ への単回帰であれば、
\begin{align}
\tilde{\boldsymbol{w}} =
\begin{bmatrix}
\tilde{a} \\ \tilde{b}
\end{bmatrix}
&= \boldsymbol{X}^* \circledast \boldsymbol{y} + \mu \\
&=
\begin{bmatrix}
-x_1 & \cdots & -x_N \\
0 & \cdots & 0
\end{bmatrix}
\circledast
\begin{bmatrix}
y_1 \\
\vdots \\
y_N
\end{bmatrix} + \mu \\
& =
\begin{bmatrix}
\min_i (y_i-x_i) + \mu \\
\min_i (y_i) + \mu
\end{bmatrix}
\end{align}
を計算すればよいわけです。

実際これで回帰を実行すると下の図のようになります。

通常の回帰直線（青）に対して、MMAEによるトロピカル回帰（緑）の方がよりデータにfitしていることがわかります。そういうデータを使ったので当然といえば当然ですが。

実装編へ続く

【理論編】ではトロピカル単回帰をどう実現するか、数学的観点から追っていきました。でもやっぱりこういうのは理論と実装の両輪が必要なんですよね。というわけで、実装や回帰結果の評価に関する具体的な話は【実装編】で述べます。

limnanthaceae.hatenablog.com

*1:P. Maragos, V. Charisopoulos and E. Theodosis, "Tropical Geometry and Machine Learning," in Proceedings of the IEEE, vol. 109, no. 5, pp. 728-755, May 2021, doi: 10.1109/JPROC.2021.3065238.

*2:ぶっちゃけトロピカルであることが何の役に立つのかはさっぱりわからない。

*3:小泉構文ではない

*4:加法をmin関数にした Min-plus代数というのもあり、これをトロピカル半環として定義する場合もあります。使用用途によって好きな方を定義して使います。後述しますが、これらは双対で、また逆行列を定義するために結局両方を考えることになります。

*5:元論文では $\boxplus$ で表記されていますが、乗法なのに加法っぽい記号を使うのが少し気持ち悪いので、本記事では $\circledcirc$ で表します。