全微分を図形的に理解する - リムナンテスは愉快な気分

※数学的な厳密性はあんまり考えていません

全微分のお気持ち

全微分とは？

$f$ を $z = f(x,y)$ みたいな関数とします。つまり、 $\mathbb{R}^2\to\mathbb{R}; (x,y)\mapsto z$ とします。このとき、 $f$ の全微分 $df$ は

$df = \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy$ と表す。

…で、この $df$ ってなんぞや、となるわけですよ。ちゃんと説明してくれないと。いや大学教授も説明してくれてたのかもしれないけど覚えてないだけかもしれない。

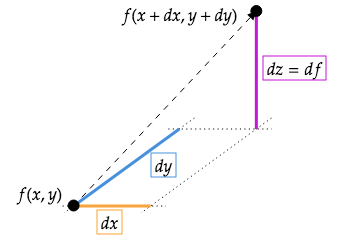
全微分で何がしたいのかというと、「 $x$ とか $y$ をちょっと増やしたら $z=f(x,y)$ の値がどのくらい増えるか？」を知りたいのである。
つまり、 $x, y$ を微小量（ $dx, dy$ ）変化させたときの $z$ の微小変化が $dz$ であり、ここでいうところの $df$ となる。

数式的に書くと、

$dz=df=f(x+dx,y+dy)-f(x,y)$
の値が知りたい、というのが全微分なんだけど、それは $f$ の偏微分をつかって計算できますよ、というのが

$df = \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy$
です。とても便利。

例えば、 $f(x,y)=-3x^2-4y^2+5xy$ の全微分は $\frac{\partial f}{\partial x} = -6x+5y, \frac{\partial f}{\partial y} = 5x-8y$ から $df = (-6x+5y)dx + (5x-8y)dy$ と計算できます。

どちらかというと熱力学でやっているみたいに、 $df = Adx + Bdy$ という式が手に入ったら、 $A, B$ が偏微分 $\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}dy$ に相当する全微分だから $f$ が復元できる…という使い方の方が実用的かもしれない。

なぜ偏微分を使って全微分 df が計算できるのか？

$\frac{\partial f}{\partial x}$ は $f$ の $x$ による偏微分、つまり $f$ の $x$ 軸方向の傾きを表します。
ということは、 $x$ 軸方向に微小量 $dx$ だけ動かした時の $f$ の変化量は $\frac{\partial f}{\partial x}dx$ です。